吴恩达机器学习

前言

• 吴恩达是一位著名的计算机科学家和机器学习专家，他是斯坦福大学的教授之一，同时也是 Coursera 上著名的机器学习课程的创始人之一。
  他的机器学习课程旨在为初学者提供深入浅出的机器学习知识，该课程涵盖了从基础的数学和统计学概念到具体算法和实践技巧等内容。该课程的主要内容包括监督学习、无监督学习、特征工程、深度学习等各个方面。

• 之前了解过一些机器学习知识，但都是零碎且片面。这次跟着吴恩达老师系统全面的学习机器学习。
  之前看视频忘记✍写笔记了，暑假打算补完。

机器学习定义

• 机器学习（Machine Learning）：是研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。一个程序被认为能从经验E中学习，解决任务 T，达到性能度量值P，当且仅当，有了经验E后，经过P评判， 程序在处理T时的性能有所提升。

• 简单来讲，机器学习：数据+算法 = 模型。通过使用某种算法（或者可以理解为策略）令计算机从数据中学习并建立模型，之后我们用这个模型来实现一些任务。比如，图像识别，房价预测等。
• 这个学习的过程就是我们常说的训练。我们希望的是这个训练好的模型，对于新的数据，可以准确实现目标任务，比如预测或分类等等。而从数据中学习所使用的算法就是机器学习研究的主要目标。
  机器学习最常见两大类型：监督学习和无监督学习

监督学习

• 监督学习（Supervised Learning）：对于数据集中每一个样本都有对应的标签，主要解决回归问题（regression）和分类问题（classification）。

• 个人理解：在监督学习中，对于给出的数据集中的样本，预测出在其他数据下我们想要的“正确答案”。
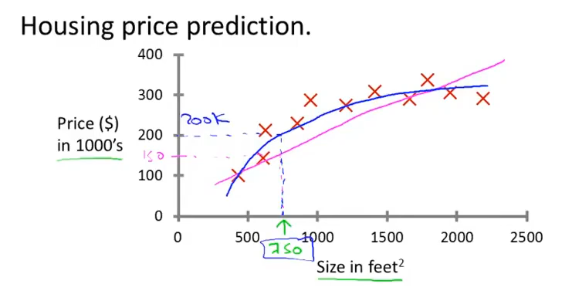
  就像回归问题（连续）：房价预测，分类问题（离散）：判断肿瘤良性还是恶性
  

无监督学习

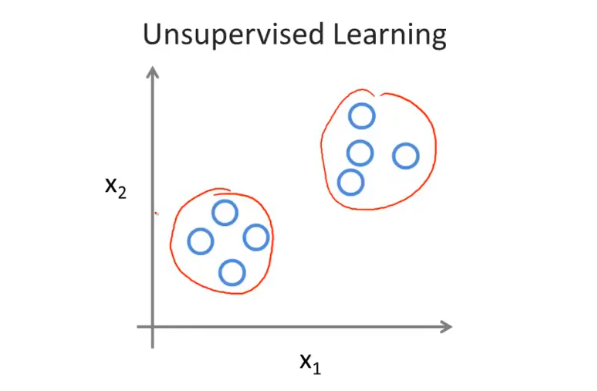
• 无监督学习（Unsupervised Learning）：数据集中没有任何的标签，让计算机自己进行学习，训练目标是能对观察值进行分类或者区分等，主要解决聚类问题（clustering）。

• 个人理解：无监督学习是不知道数据具体的含义，比如给定一些数据但不知道它们具体的信息，对于分类问题无监督学习可以得到多个不同的聚类，从而实现预测的功能。
  

线性回归

单元线性回归

• 假设函数：

$$h_\theta(x)=\theta_0+\theta_1x$$

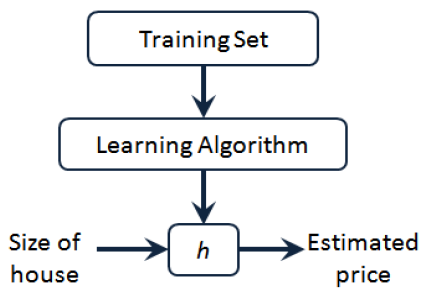
• 给定训练样本$(x^i,y^i)$，其中：$i=1,2,...,m$,$x$表示特征，$y$表示输出目标，监督学习算法的工作方式如图所示：
  

代价函数

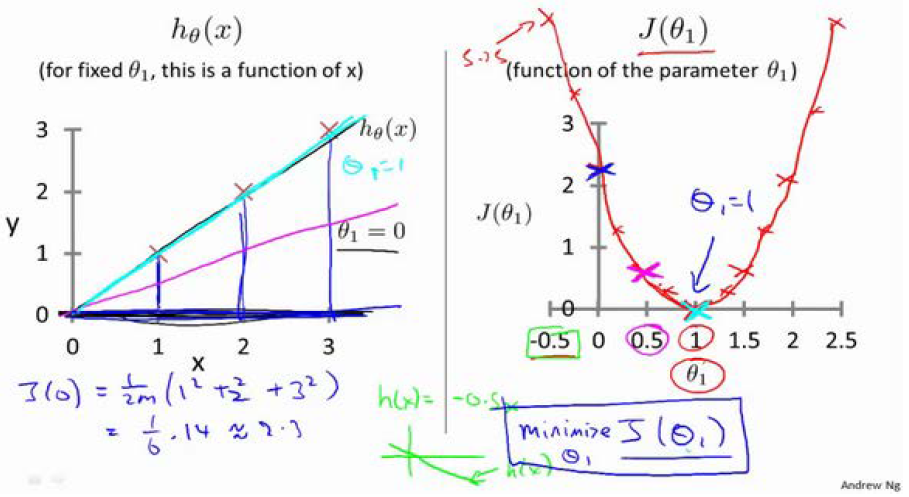
• 代价函数（cost function）:

$$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h(x^i)-y^i)^2$$

训练的目标为最小化代价函数，即找到假设函数中的最优参数

$$\underset{\theta_0,\theta_1}{minimize}J(\theta_0,\theta_1)$$

梯度下降

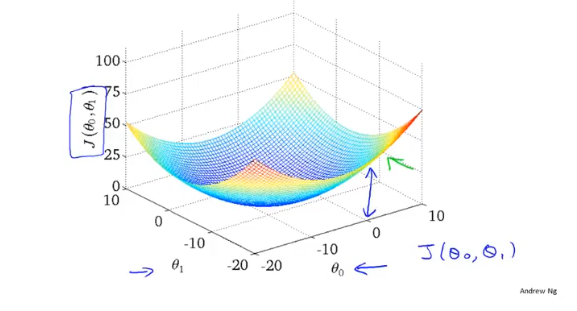
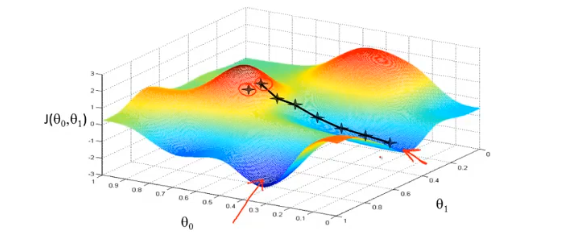
• 首先为每个参数赋一个初值，通过代价函数的梯度，然后不断地调整参数，最终得到一个局部最优解。
  贪心算法，初值的不同可能会得到两个不同的结果，即梯度下降不一定得到全局最优解。

$$\theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$$

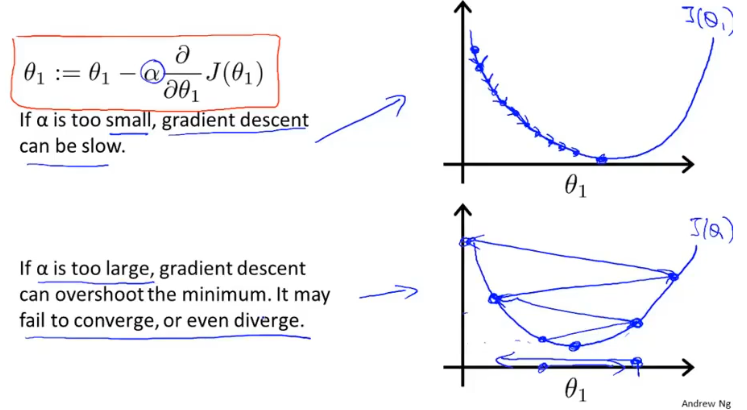
$\alpha$为学习速率（learning rate），即更新步长。

• 梯度下降公式中有两个部分，学习率和偏导数。

• $\alpha$为学习率（learning rate），即更新步长。如果太小则需要很多步才能收敛，如果太大最后可能不会收敛甚至可能发散。
  

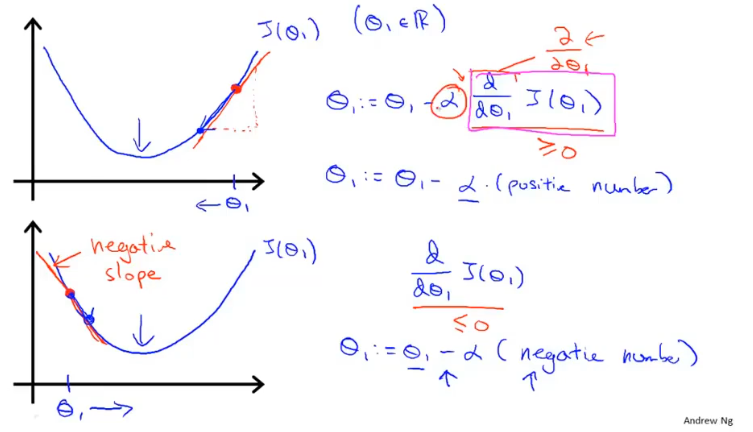
• 偏导数，用来计算当前参数对应代价函数的斜率，导数为正则$\theta$减小，导数为负则$\theta$增大，通过这样的方式可以使整体向$\theta=0$收敛。
  

• 当$\theta$处于局部最优解时，$\theta$的值将不再更新，因为偏导为0。
• 梯度下降在具体的执行时，每一次更新需要同时更新所有的参数。
  
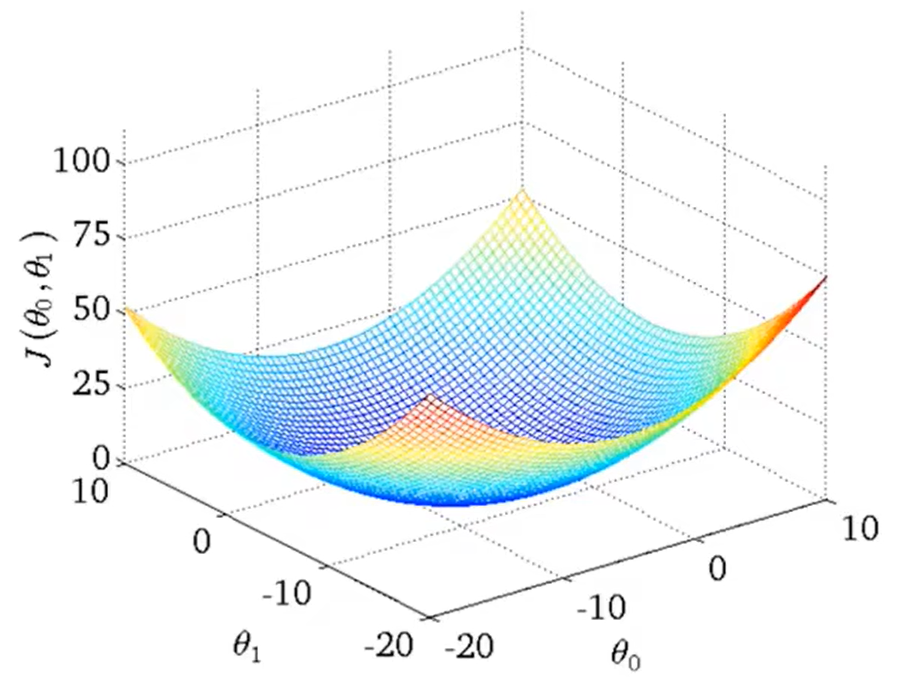
• 梯度下降的过程容易出现局部最优解,但是线性回归的代价函数，往往是一个凸函数。它总能收敛到全局最优。

多元线性回归

• 假设函数：(定义$x_0=1$)

$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n$$

• 代价函数：

$$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h\theta(x^{(i)})-y^{(i)})^2$$

• 梯度下降公式：

$$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta),j=0,1,\ldots,n$$

猜你想看：进度测验

对监督学习和非监督学习的认识

• 监督学习

  在监督学习中，对于给出的数据集中的样本，预测出在其他数据下我们想要的“正确答案”。

  也就是已经有打好答案标签的训练集，学习其中的特征，当给出新的数据时能够做出正确判断。

  经典应用有：回归问题（连续），分类问题：判断肿瘤良性还是恶性。

• 非监督学习

  无监督学习是不知道数据具体的含义，对于分类问题无监督学习可以得到多个不同的聚类簇，从而实现预测的功能。

  经典应用有：聚类问题

Machine Learning梯度下降算法实现的过程

• 梯度下降其实就是一种自动求最优参数的一种方法,运用贪心思想，能够得到局部最优解，但注意不一定是全局最优解

（这里以单元线性回归为例子）

• 假设函数

$$h_\theta(x)=\theta_0+\theta_1x$$

• 代价函数

$$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h(x^i)-y^i)^2$$

• 我们要找到$\theta_0\theta_1$的某种取值组合，使代价函数$J(\theta_0,\theta_1)$有最小值

$$\underset{\theta_0,\theta_1}{minimize}J(\theta_0,\theta_1)$$

• 梯度下降法(通过代价函数的梯度，然后不断地调整参数，最终得到一个局部最优解。)

• step1：为每个参数$\theta_0\theta_1$赋初值(一般都为0)。

• step2：$\theta_0\theta_1$分别求偏导。

$$\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})$$

$$\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})\cdot x^{(i)}$$

• step3：$\theta_0\theta_1$分别减去对应偏导乘学习率$\alpha$。（同步更新）

$$\theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$$

注：线性回归的代价函数$J(\theta_0,\theta_1)$为凸函数，其局部最优解就是全局最优解